半導体集積回路 第2講
2 低消費電力
2.1 何が問題?
私の研究テーマは「低消費電力」。消費電力って何とか聞かないでくださいね。中学で習ったあれです。(電力=電流×電圧。)思い出しました?要するに消費する電気の量のことです。家電の仕様書を見れば、TVは100W(ワット)とかレンジは500Wとか書いてありますよね。ちなみに、インテルCPUの消費電力は数十W、なんだ、少ないじゃんと思わないでください。TVやレンジはあれだけでっかくて数百Wです。でも、CPUは手のひらより小さいんですよ。パソコンの中を見たことがある人はわかると思いますが、小型のファンの下にくっついている板みたいなやつがCPUです。あんな小さいものが数十Wの電力を消費したら大変なことです。中心部の温度は100度近く。卵だって焼けちゃいます。実際、チップ内部の局所的な温度は現在ホットプレートと同じくらいの熱さであり、将来は原子炉と同程度のエネルギー密度に達するそうです。あなたのコンピュータの中に原子炉が!?信じられますか。こんなものを高温のままほうっておいたらすぐに壊れてしまうので、CPUの上にファンをくっつけて常にまわして冷やすわけです。
現在、CPUのメーカーは各社競いあってより周波数の高い製品を作ろうとしています。最新のPentium4は2.0GHzですが来年には3.0GHzもでるでしょう(2001年9月現在。記事が古かったらごめんなさい)。性能はあがっていいことですが、それに伴って消費電力も増大します。もし消費電力が大きくなったらもっと大きくて強力なファンをつけなければいけません。CPUは豆粒ほどなのに、ファンはこぶしよりでかい。コンピュータから聞こえてくる定常的な雑音はファンの音です。夏は当然がんがんクーラーをきかせる必要があります。そして、電気量ははねあがりあなたの家計を圧迫します。何も対策を施さないでほおっておくと、将来はパソコン関連の消費電力が家庭の全消費電力の大半を占めるなんていうことになりかねません。
携帯電話のような携帯機器の場合は事態はもっと深刻です。携帯電話の消費電力は最高でも数W程度ですが、もっと消費電力があがると電池をすぐに消耗してしまい使用できる時間が短くなってしまいます。毎日、家に帰ったらすぐに携帯を充電というのも嫌ですよね。それにパソコンのCPUのようにファンをつけるわけにはいかないので過度に発熱すれば皮膚の低温やけどもあるかもしれません。
というわけで、チップの消費電力を減らすための研究はとても重要なのです。どうやって消費電力を減らすのかについてはこれから詳しくみていきましょう。
2.2 消費電力
ところで、みなさんは物理を学んだことがありますか。力学だけじゃなくて電磁気学まで学んであると説明がとっても楽なんですけれど、たぶんほとんどの人は物理の教科書すら見たことがないと思うので、ここは水とマスを用いて説明します。なお、以下の説明はあくまでも理解しやすくするための説明であり、実際の電子回路の
動作とは若干異なります。
水と電気はまったく異なるものですが、物理的には同等の概念で説明できます。電気は目に見えず説明しづらいので水で説明します。水の流れが電流、マスにためられる水が電荷(電気)だと思ってください。
下図(a)をご覧ください。底面積C、高さVのマスがあり、そこへ水源からポンプで水が供給されるとします。マスはポンプをのつけ口以外はすべてふさがれていて水の出口はありません。水はポンプでマスの高さと同じ高さVまで引き上げられマスの中に注入されます。ポンプには弁がついており、弁とひもでつながっている別のマスの働きで弁が開閉します。こちらのマスを弁開閉マスとします。(注:
この図にはちょっと不備がありますがご了承ください。後で直す予定です。)
最初はマスの中に水は入っていません。この状態をディジタルであらわすと"0"です。一方、弁開閉マスにも水がはいっていない、つまり"0"の状態で、弁は閉じています。
弁開閉マスに水が満たされる、つまり"1"の状態になると、弁が開いてポンプに水が流れマスに水が注入され始めます(図(b))。ポンプは常に一定量で水が流れ、1秒間にポンプ内を流れる水の量を
I とします。
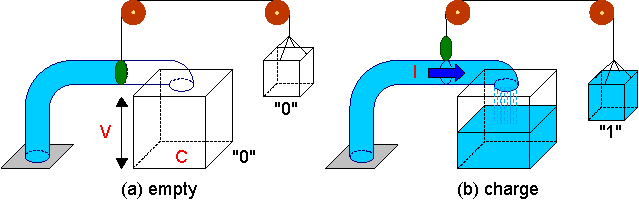
やがて、マスの中に水がいっぱいになります(図(c))。この状態をディジタルであらわすと"1"です。これ以上は水が入らないのでポンプの水の流れは止まります。蓄えられた水の量はマスの体積分であるQ=CVとなります。(Cは底面積、Vは高さだから。)
次に弁開閉マスが"0"になって弁は閉じ、マスの下にある穴をあけてマスの中の水を捨てます(図(d))。
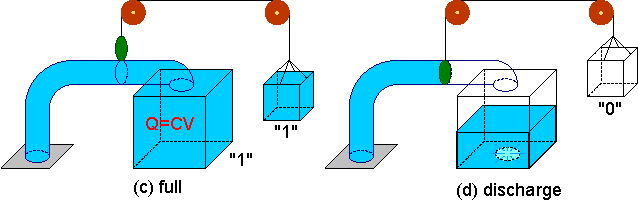
これが1サイクルで電子回路が行っていることです。水のかわりに電荷がいっぱいに供給されたら"1"のデータになり、電荷を捨てれば"0"のデータになります。"0"と"1"のディジタルデータを集積回路内ではこのようにしてあらわしています。
さて、ここでどれだけの電力(水力)が消費されるかを考えてみましょう。1サイクルの中で水力が消費されているのは、図(b)で水をポンプで引き上げるところです。水をポンプで高さVまで引き上げるには当然エネルギーを必要とします。ここで、重要な物理法則ですが必要なエネルギー量は引き上げる高さに比例します。供給した水の量はQ=CV、それを高さVまで引き上げたので、要したエネルギーは
CV × V = CV2 となります。
ところで消費水力(電力)とは、1秒間に消費されるエネルギーのことをいいます。水を供給するのに
T 秒かかったとすると、消費水力を P として P = CV2/T
となります。T を物理用語では周期といいます。
水を引き上げるスピードは日常の範囲では何秒、何十秒の単位ですが、電子のスピードは非常に高速で1サイクルあたりにかかる時間は何億分の1秒という単位なので、集積回路の分野では、通常、周期
T ではなく周波数 f
を用います。周波数とは1秒間に何回動作を繰り返すかをあらわす単位で、周期
T とは f = 1/T の関係があります。例をとると、T=10秒なら
f=0.1Hzですし、T=0.001秒なら f=1,000Hz(1KHz)です。
結局、消費水力(電力)は P = fCV2
とあらわされます。
ここで、説明に用いた水と、電気の各パラメータの関係を対応させて整理しておきます。厳密にはちょっと違いますが、まあ以下のように対応づけることができるでしょう。
| パラメータ |
水 |
電気 |
説明 |
| V |
水の高さ |
電圧 |
ポテンシャル、潜在的な力 |
| I |
水流 |
電流 |
1秒あたりに流れる量 |
| P |
水力 |
電力 |
1秒あたりに消費されるエネルギー |
| C |
マスの底面積 |
容量 |
定数 |
| Q |
マス内の水量 |
電荷量 |
Q = CV |
電圧とは電気がどれだけの力をなしえるか、どれだけの力を潜在的に秘めているかをあらわしています。水の場合だと高い位置にあればあるほど大きな力を秘めており、落ちれば大きな力を発揮します。電気の場合だと電圧は電子にとっての高さというわけです。電流は水流と同じく1秒あたりに流れる量。電力は電流が流れているときに1秒あたりに消費されるエネルギー。容量は電気が流れる媒体に応じて決まる定数。電荷量は電極にたまる正と負の電荷の量です。ここでは水を例にとりマスにたまる水の量として説明しましたが、電気の場合はある離れた二つの金属の片方に正の電荷がもう片方に負の電荷がたまります。つまり帯電します。
あとは話すと長くなりそうだし、図を書くのも面倒なので省略します。消費電力
P = fCV2
だと覚えておいてください。
参考:
中学の理科の授業で、電力 P =電圧 V ×電流 I
と習ったと思います。なのに、ここでは P = fCV2
という式がでてきてなんで違うんだと思われるかもしれませんが、どちらも正しい式です。着目している個所が違うだけです。前者の
P=VI
は電源に着目した式です。先ほどの水の例ではポンプで水を引き上げるのに消費されている力です。一方、後者の
P = fCV2
はたまった電荷に着目した式です。水の例では、水をためるのに必要な力です。水が外に漏れなければ、ポンプで水を引き上げるのに消費する力と水をためるのに消費する力は同じなので、両者はどちらも正しい式です。
両者の式はちょこちょっとした計算で簡単に変換できます。1秒間に流れる水量を I
、水量 Q の水をためるのにかかる時間を T
としたので、供給された水の量に関して I
× T = Q = CV、すなわち I = CV/T 。周波数と周期の f = 1/T
の関係から I = fCV 。これを P = VI に代入して P = fCV2
です。ただし、ここでは水流 I
は一定として計算しています。実際の電気回路では、電流 I
は指数関数的に変化するので、微分積分を用いた計算が必要ですが、ここでは省略します。
2.3 消費電力の削減
さて、消費電力が何かわかったところで(わかっていなくても)、どうやって消費電力を削減するのかについて見ていきましょう。前節の消費電力の式を思い出してください。
P = fCV2
電力 P は周波数 f 、容量 C 、電圧 V
の関数です。このどれかを小さくすれば P
を少なくできます。さて、どれを少なくしましょうか。
周波数 f
を小さくするのはちょっと無理そうですね。動画像や音楽の処理、ネットゲームなどで今はみんなもっともっと高速で動くチップを欲しがっていますからね。GHz時代にいまさら100MHzのプロセッサなんて使えないでしょう。
それでは 容量C
を少なくしましょうか。容量といっても電磁気学を習っていない人にはまったくイメージがわかないと思いますが、まあ前節の水の例でいえばマスの底面積みたいにある物に固有な値です。簡単に言えば物を小さくすれば容量は小さくなります。じゃあ小さくすればいいじゃないというわけで、多くの半導体技術者が苦労してトランジスタや配線をどんどん小さくしています。ただ、デバイスそのものを改良するので設計屋さんの私の研究室ではできません。(うちの研究室はいわゆる理系の実験室のイメージとは違い、各人の机と棚、そして研究に欠かせないコンピュータがならんだオフィスです。薬品も巨大な実験装置もありません。)
そこで、私の研究室では、電圧V
を小さくします。正確にいうと電圧を小さくしても正常に動作する回路方式を考えるわけです。例えば水車にたとえれば、水の高さを単に低くするだけだと水車はのろくなるので、水の受け方を変えたり水車の置く位置を変えたり、または水車の先につながるなんかの機械を調整して水車がのろくても機械は正常に動くようにします。さらに、電圧を小さくすることの大きな利点は、
P = fCV2
の式を見るとわかりますが、電力 P は電圧 V
の2乗に比例して小さくなることです。
電圧Vの詳細な落とし方については、話が専門的になりますので、省略します。ここでは、電圧を落とせば消費電力を削減できると覚えておいてください。もし、Impress社のPower
Report
なんていうちょっとマニアな雑誌を愛読されている方なら、CPUの周波数があがっても消費電力は比例してあがってはいないことにお気付きでしょう。これは、周波数があがっても電源電圧が落ちているので結果的に消費電力が抑えられているからです。
次は日常的な研究でどんなことをしているのか紹介します。
研究のページのトップへ


